Параболическая формула Джонсона

В строительной инженерии параболическая формула Джонсона — это эмпирически обоснованное уравнение для расчета критического напряжения прогиба колонны. Формула основана на экспериментальных результатах Дж. Б. Джонсона, полученных около 1900 года, как альтернатива формуле критической нагрузки Эйлера в условиях низкого коэффициента гибкости (отношение радиуса инерции к эффективной длине).
Уравнение интерполирует между пределом текучести материала и критическим напряжением прогиба, заданным формулой Эйлера, связывающей коэффициент гибкости с напряжением, необходимым для прогиба колонны.

Выпучивание относится к режиму разрушения, при котором конструкция теряет устойчивость. Это связано с недостаточной жесткостью конструкции. Установка нагрузки на длинный тонкий стержень может привести к разрушению коробления до того, как образец выйдет из строя при сжатии.

Парабола Джонсона

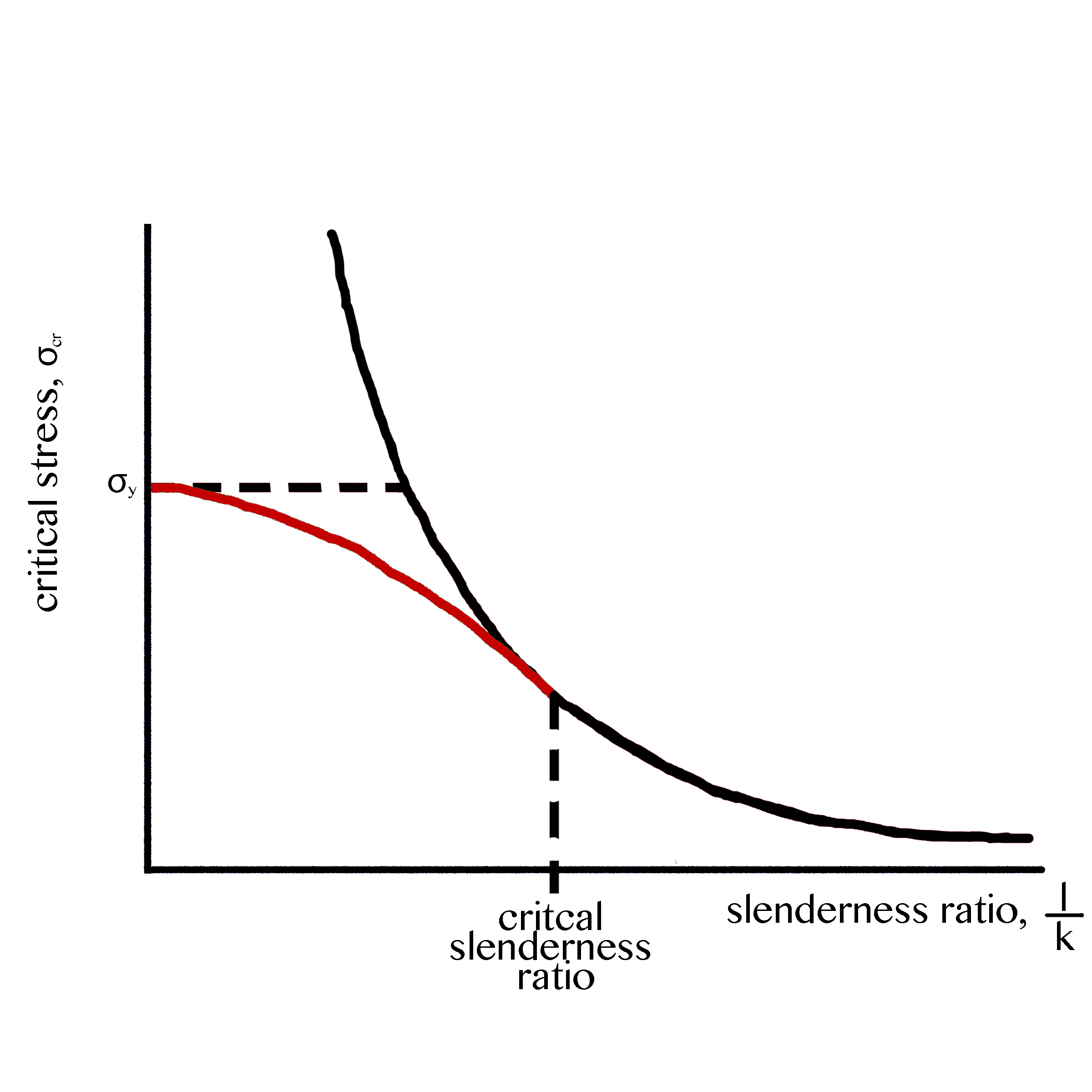
Формула Эйлера для потери устойчивости тонкой колонны дает критический уровень напряжения, вызывающий потерю устойчивости, но не учитывает режимы разрушения материала, такие как текучесть, которая, как было показано, снижает критическое напряжение потери устойчивости. Формула Джонсона интерполирует между пределом текучести материала колонны и критическим напряжением, заданным формулой Эйлера. Она создает новую границу отказа, подгоняя параболу к графику отказа для потери устойчивости Эйлера с помощью

${\displaystyle \sigma _{cr}=\sigma _{y}-{1 \over E}{\left({\frac {\sigma _{y}}{2\pi }}\right)}^{2}{\left({\frac {l}{k}}\right)}^{2}}$

${\displaystyle \sigma _{cr}=\sigma _{y}-{1 \over E}{\left({\frac {\sigma _{y}}{2\pi }}\right)}^{2}{\left({\frac {l}{k}}\right)}^{2}}$

На графике кривой Эйлера имеется точка перехода, расположенная на критическом коэффициенте гибкости. При значениях гибкости ниже этой точки (встречающихся в образцах с относительно короткой длиной по сравнению с их поперечным сечением) график будет следовать параболе Джонсона; напротив, большие значения гибкости будут более точно соответствовать уравнению Эйлера.

Формула Эйлера:

${\displaystyle \sigma _{cr}={P_{cr} \over A}={\pi ^{2}EI \over AL_{e}^{2}}={\pi ^{2}E \over \left({\frac {l}{k}}\right)^{2}}}$

где

${\displaystyle \sigma _{cr}=}$ critical stress,

${\displaystyle P_{cr}=}$ critical force,

${\displaystyle A=}$ area of cross section,

${\displaystyle L_{e}=}$ Effective length of the rod,

${\displaystyle E=}$ modulus of elasticity,

${\displaystyle I=}$ area moment of inertia of the cross section of the rod,

${\displaystyle {l \over k}}$ = slenderness ratio.

Уравнение Эйлера полезно в таких ситуациях, как идеальный закрепленный-закрепленный столбец, или в случаях, когда эффективную длину можно использовать для корректировки существующей формулы (т. е. фиксированно-свободный).

(L — исходная длина образца до приложения силы.)

Однако некоторые геометрии неточно представлены формулой Эйлера. Одной из переменных в приведенном выше уравнении, которая отражает геометрию образца, является коэффициент гибкости, который представляет собой длину колонны, деленную на радиус инерции.

Коэффициент гибкости является показателем сопротивления образца изгибу и выпучке, обусловленным его длиной и поперечным сечением. Если коэффициент гибкости меньше критического коэффициента гибкости, колонна считается короткой. В этих случаях парабола Джонсона более применима, чем формула Эйлера. Коэффициент гибкости члена можно найти с помощью ${\displaystyle \left({\frac {l}{k}}\right)=L_{e}{\sqrt {A \over I}}}$

Критический коэффициент гибкости равен

${\displaystyle \left({\frac {l}{k}}\right)_{cr}={\sqrt {2\pi ^{2}E \over \sigma _{y}}}}$

Пример

Одним из распространенных материалов в аэрокосмической промышленности является алюминий 2024. Некоторые свойства алюминия 2024 были определены экспериментально, такие как предел текучести при растяжении (324 МПа) и модуль упругости (73,1 ГПа). Формулу Эйлера можно использовать для построения кривой отказов, но она не будет точной ниже определенного ${\displaystyle {\frac {l}{k}}}$ значение, критический коэффициент гибкости.

${\displaystyle {\left({\frac {l}{k}}\right)}_{cr}={\sqrt {2\pi ^{2}E \over \sigma _{y}}}={\sqrt {\frac {2\pi ^{2}\times 73.1\times 10^{9}}{324\times 10^{6}}}}=66.7}$

${\displaystyle {\left({\frac {l}{k}}\right)}_{cr}={\sqrt {2\pi ^{2}E \over \sigma _{y}}}={\sqrt {\frac {2\pi ^{2}\times 73.1\times 10^{9}}{324\times 10^{6}}}}=66.7}$

Следовательно, уравнение Эйлера применимо для значений ${\displaystyle {\frac {l}{k}}}$ больше 66,7.

Euler: ${\displaystyle \sigma _{cr}={\pi ^{2}E \over \left({\frac {l}{k}}\right)^{2}}={\pi ^{2}\times 73.1\times 10^{9} \over \left({\frac {l}{k}}\right)^{2}}}$ for ${\displaystyle {\frac {l}{k}}>66.7}$

(units in Pascals)

Euler: ${\displaystyle \sigma _{cr}={\pi ^{2}E \over \left({\frac {l}{k}}\right)^{2}}={\pi ^{2}\times 73.1\times 10^{9} \over \left({\frac {l}{k}}\right)^{2}}}$ for ${\displaystyle {\frac {l}{k}}>66.7}$

(units in Pascals)

(units in Pascals)

Парабола Джонсона учитывает меньшие ${\displaystyle {\frac {l}{k}}}$ значения.

Johnson: ${\displaystyle \sigma _{cr}=\sigma _{y}-{1 \over E}{\left({\frac {\sigma _{y}}{2\pi }}\right)}^{2}{\left({\frac {l}{k}}\right)}^{2}=324\times 10^{6}-{1 \over 73.1\times 10^{9}}{\left({\frac {324\times 10^{6}}{2\pi }}\right)}^{2}{\left({\frac {l}{k}}\right)}^{2}}$ for ${\displaystyle 0\leq {\frac {l}{k}}\leq 66.7}$

Johnson: ${\displaystyle \sigma _{cr}=\sigma _{y}-{1 \over E}{\left({\frac {\sigma _{y}}{2\pi }}\right)}^{2}{\left({\frac {l}{k}}\right)}^{2}=324\times 10^{6}-{1 \over 73.1\times 10^{9}}{\left({\frac {324\times 10^{6}}{2\pi }}\right)}^{2}{\left({\frac {l}{k}}\right)}^{2}}$ for ${\displaystyle 0\leq {\frac {l}{k}}\leq 66.7}$

(units in Pascals)

(units in Pascals)

(units in Pascals)