Акустоэластичный эффект

Акустоупругий эффект заключается в том, как изменяются скорости звука (как продольные, так и сдвиговые) в упругом материале, если он подвергается воздействию начального статического поля напряжений. Это нелинейный эффект определяющего соотношения между механическим напряжением и конечной деформацией в материале непрерывной массы. В классической линейной теории упругости малые деформации большинства упругих материалов можно описать линейным соотношением между приложенным напряжением и результирующей деформацией. Это соотношение обычно известно как обобщенный закон Гука. Линейная теория упругости включает упругие константы второго порядка (например,

λ

{\displaystyle \lambda }

и

μ

{\displaystyle \mu }

) и дает постоянные продольные и сдвиговые скорости звука в упругом материале, не подверженном влиянию приложенного напряжения. Акустоупругий эффект, с другой стороны, включает расширение более высокого порядка определяющего соотношения (нелинейной теории упругости) между приложенным напряжением и результирующей деформацией, что дает продольные и сдвиговые скорости звука, зависящие от напряженного состояния материала. В пределе ненапряженного материала воспроизводятся скорости звука линейной теории упругости.

Акустоупругий эффект был исследован еще в 1925 году Бриллюэном. Он обнаружил, что скорость распространения акустических волн уменьшается пропорционально приложенному гидростатическому давлению. Однако следствием его теории стало то, что звуковые волны прекращают распространяться при достаточно большом давлении. Позднее было показано, что этот парадоксальный эффект вызван неверными предположениями о том, что упругие параметры не зависят от давления.

В 1937 году Фрэнсис Доминик Мурнаган представил математическую теорию, расширяющую линейную теорию упругости, включив в нее также конечную деформацию в упругих изотропных материалах. Эта теория включала три упругие константы третьего порядка ${\displaystyle l}$, < span class="mwe-math-element">${\displaystyle m}$< img alt="{\displaystyle m}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert Skin-invert" src="https://.org/api/rest_v1/ media/math/render/svg/0a07d98bb302f3856cbabc47b2b9016692e3f7bc" style="vertical-align: -0.338ex; ширина:2.04ex; высота:1.676ex;"/> и ${\displaystyle n}$. В 1953 году Хьюз и Келли использовали теорию Мурнагана в своей экспериментальной работе, чтобы установить числовые значения упругих констант более высокого порядка для нескольких упругих материалов, включая полистирол, железо Armco и пирекс, подвергнутых гидростатическому давлению и одноосному сжатию.

Нелинейная теория упругости для гиперупругих материалов

Акустоупругий эффект — это эффект конечной деформации нелинейных упругих материалов. Современное всестороннее изложение этого можно найти в. В этой книге рассматривается применение нелинейной теории упругости и анализ механических свойств твердых материалов, способных к большим упругим деформациям. Частный случай акустоупругой теории для сжимаемого изотропного гиперупругого материала, такого как поликристаллическая сталь, воспроизведен и показан в этом тексте из нелинейной теории упругости, представленной Огденом.

Note that the setting in this text as well as in is isothermal, and no reference is made to thermodynamics.

Определяющее соотношение – гиперупругие материалы (соотношение напряжение-деформация)

Гиперупругий материал — это особый случай упругого материала Коши, в котором напряжение в любой точке является объективным и определяется только текущим состоянием деформации относительно произвольной опорной конфигурации (более подробную информацию о деформации см. также на страницах Деформация (механика) и Конечная деформация). Однако работа, выполняемая напряжениями, может зависеть от пути деформации. Поэтому упругий материал Коши имеет неконсервативную структуру, и напряжение не может быть выведено из скалярной функции упругого потенциала. Особый случай упругих материалов Коши, в котором работа, выполняемая напряжениями, не зависит от пути деформации, называется упругим материалом Грина или гиперупругим материалом. Такие материалы являются консервативными, и напряжения в материале могут быть выведены с помощью скалярного упругого потенциала, более известного как функция плотности энергии деформации.

Конститутивная связь между напряжением и деформацией может быть выражена в различных формах в зависимости от выбранных форм напряжения и деформации. Выбор 1-го тензора напряжений Пиолы-Кирхгофа ${\displaystyle {\boldsymbol {P}}}$ (который является транспонированным тензором номинального напряжения ${\displaystyle {\boldsymbol {P}}^{T}={\boldsymbol {N}}}$), уравнение состояния для сжимаемого гиперупругого материала может быть выражено в терминах лагранжевой деформации Грина (${\displaystyle {\boldsymbol {E}}}$) как:
$${\displaystyle {\boldsymbol {P}}={\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {E}}}}\qquad {\text{or}}\qquad P_{ij}=F_{ik}~{\frac {\partial W}{\partial E_{kj}}},\qquad i,j=1,2,3~,}$$
где ${\displaystyle {\boldsymbol {F}}}$ — тензор градиента деформации, а второе выражение использует соглашение Эйнштейна о суммировании для индексной записи тензоров. ${\displaystyle W}$ — это функция плотности энергии деформации для гиперупругого материала, которая была определена на единицу объема, а не на единицу массы, поскольку это позволяет избежать необходимости умножать правую часть на плотность массы ${\displaystyle \rho _{0}}$ эталонной конфигурации.

Предполагая, что скалярная функция плотности энергии деформации ${\displaystyle W({\boldsymbol {E}})}$ может быть аппроксимирована с помощью разложения в ряд Тейлора в текущей деформации ${\displaystyle {\boldsymbol {E}}}$, его можно выразить (в индексной нотации) как:
$${\displaystyle W\approx C_{0}+C_{ij}E_{ij}+{\frac {1}{2!}}C_{ijkl}E_{ij}E_{kl}+{\frac {1}{3!}}C_{ijklmn}E_{ij}E_{kl}E_{mn}+\cdots }$$
Наложение ограничений, что функция энергии деформации должна быть равна нулю и иметь минимум, когда материал находится в недеформированном состоянии (т. е. ${\displaystyle W(E_{ij}=0)=0}$) ясно, что в функции энергии деформации нет постоянного или линейного члена, и таким образом:
$${\displaystyle W\approx {\frac {1}{2!}}C_{ijkl}E_{ij}E_{kl}+{\frac {1}{3!}}C_{ijklmn}E_{ij}E_{kl}E_{mn}+\cdots ,}$$
где ${\displaystyle C_{ijkl}}$ — тензор четвертого порядка модулей упругости второго порядка, в то время как ${\displaystyle C_{ijklmn}}$ — тензор шестого порядка модулей упругости третьего порядка.
Симметрия ${\displaystyle E_{ij}=E_{ji}}$ вместе со скалярной функцией плотности энергии деформации ${\displaystyle W}$ подразумевает, что модули второго порядка ${\displaystyle C_{ijkl}}$ имеют следующую симметрию:
$${\displaystyle C_{ijkl}=C_{jikl}=C_{ijlk},}$$
которые уменьшают количество независимых упругих констант с 81 до 36. Кроме того, степенное разложение подразумевает, что модули второго порядка также имеют главную симметрию
$${\displaystyle C_{ijkl}=C_{klij},}$$
что еще больше сокращает число независимых упругих констант до 21. Те ​​же аргументы можно использовать для модулей упругости третьего порядка ${\displaystyle C_{ijklmn}}$. Эти симметрии также позволяют выразить упругие модули с помощью нотации Фойгта (т. е. ${\displaystyle C_{ijkl}=C_{IJ}}$ и ${\displaystyle C_{ijklmn}=C_{IJK}}$).

Тензор градиента деформации можно выразить в компонентной форме как
$${\displaystyle F_{ij}={\frac {\partial u_{i}}{\partial X_{j}}}+\delta _{ij},}$$
где ${\displaystyle u_{i}}$ это смещение материальной точки ${\displaystyle P}$ от координаты ${\displaystyle X_{i}}$ в опорной конфигурации для координации ${\displaystyle x_{i}}$ в деформированной конфигурации (см. рисунок 2 на странице теории конечных деформаций). Включение степенного разложения функции энергии деформации в определяющее соотношение и замена тензора деформации Лагранжа ${\displaystyle E_{kl}}$ с расширением, указанным на странице тензора конечной деформации, получается (обратите внимание, что строчные буквы ${\displaystyle u}$ были использованы в этом разделе по сравнению с заглавными буквами на странице конечной деформации) основное уравнение
$${\displaystyle P_{ij}=C_{ijkl}{\frac {\partial u_{k}}{\partial X_{l}}}+{\frac {1}{2}}M_{ijklmn}{\frac {\partial u_{k}}{\partial X_{l}}}{\frac {\partial u_{m}}{\partial X_{n}}}+{\frac {1}{3}}M_{ijklmnpq}{\frac {\partial u_{k}}{\partial X_{l}}}{\frac {\partial u_{m}}{\partial X_{n}}}{\frac {\partial u_{p}}{\partial X_{q}}}+\cdots ,}$$
где
$${\displaystyle M_{ijklmn}=C_{ijklmn}+C_{ijln}\delta _{km}+C_{jnkl}\delta _{im}+C_{jlmn}\delta _{ik},}$$
и члены более высокого порядка были проигнорированы
(см. подробные выводы).
Для справкиM путем пренебрежения членами более высокого порядка в ${\displaystyle \partial u_{k}/\partial X_{l}}$ это выражение сокращается до
${\displaystyle P_{ij}=C_{ijkl}{\frac {\partial u_{k}}{\partial X_{l}}},}$
который является версией обобщенного закона Гука, где ${\displaystyle P_{ij}}$ является мерой напряжения, в то время как ${\displaystyle \partial u_{k}/\partial X_{l}}$ является мерой деформации, а ${\displaystyle C_{ijkl}}$ — линейная связь между ними.

Скорость звука

Предполагая, что малая динамическая (акустическая) деформация возмущает уже статически напряженный материал, акустоупругий эффект можно рассматривать как эффект малой деформации, наложенной на большую конечную деформацию (также называемую теорией малого на большом). Определим три состояния данной материальной точки. В исходном (ненапряженном) состоянии точка определяется координатным вектором ${\displaystyle {\boldsymbol {X}}}$, в то время как та же точка имеет вектор координат ${\displaystyle {\boldsymbol {x}}}$ в статическом изначально напряженном состоянии (т. е. под воздействием приложенного предварительного напряжения). Наконец, предположим, что материальная точка под малым динамическим возмущением (полем акустических напряжений) имеет координатный вектор ${\displaystyle {\boldsymbol {x’}}}$. Полное смещение материальных точек (под влиянием как статического предварительного напряжения, так и динамического акустического возмущения) может быть описано векторами смещения
$${\displaystyle {\boldsymbol {u}}={\boldsymbol {u}}^{(0)}+{\boldsymbol {u}}^{(1)}={\boldsymbol {x’}}-{\boldsymbol {X}},}$$
где
$${\displaystyle {\boldsymbol {u}}^{(0)}={\boldsymbol {x}}-{\boldsymbol {X}},\qquad {\boldsymbol {u}}^{(1)}={\boldsymbol {x’}}-{\boldsymbol {x}}}$$
описывает статическое (лагранжево) начальное смещение из-за приложенного предварительного напряжения и (эйлерово) смещение из-за акустического возмущения соответственно.
Первый закон движения Коши (или баланс линейного импульса) для дополнительного эйлерова возмущения ${\displaystyle {\boldsymbol {u}}^{(1)}}$ затем можно вывести в терминах промежуточной лагранжевой деформации ${\displaystyle {\boldsymbol {u}}^{(0)}}$ предполагая, что предположение о малом на большом
$${\displaystyle |{\boldsymbol {u}}^{(1)}|\ll |{\boldsymbol {u}}^{(0)}|}$$
выдерживает.
Используя лагранжеву форму первого закона движения Коши, где эффект постоянной объемной силы (т. е. гравитация) была проигнорирована, дает
$${\displaystyle \operatorname {Div} {\boldsymbol {P}}=\rho _{0}{\ddot {{\boldsymbol {x}}’}}.}$$

Note that the subscript/superscript «0» is used in this text to denote the un-stressed reference state, and a dotted variable is as usual the time (

t

{\displaystyle t}

) derivative of the variable, and ${\displaystyle \operatorname {Div} }$ is the divergence operator with respect to the Lagrangian coordinate system ${\displaystyle {\boldsymbol {X}}}$.

Правая часть (часть, зависящая от времени) закона движения может быть выражена как
$${\displaystyle {\begin{aligned}\rho _{0}{\ddot {{\boldsymbol {x}}’}}&=\rho _{0}{\frac {\partial ^{2}}{\partial t^{2}}}({\boldsymbol {u}}^{(0)}+{\boldsymbol {u}}^{(1)}+{\boldsymbol {X}})\\&=\rho _{0}{\frac {\partial ^{2}{\boldsymbol {u}}^{(1)}}{\partial t^{2}}}\end{aligned}}}$$
в предположении, что как ненапряженное состояние, так и начальное состояние деформации являются статическими и, таким образом, ${\textstyle \partial ^{2}{\boldsymbol {u}}^{(0)}/\partial t^{2}=\partial ^{2}{\boldsymbol {X}}/\partial t^{2}=0}$.

Для левой части (часть, зависящая от пространства) пространственные частные производные Лагранжа относительно ${\displaystyle X_{j}}$ можно развернуть в эйлеровом ${\displaystyle x_{j}}$ с помощью цепочки правило и изменение переменных через отношение между векторами смещения как
$${\displaystyle {\frac {\partial }{\partial X_{j}}}={\frac {\partial }{\partial x_{j}}}+u_{k,j}^{(0)}{\frac {\partial }{\partial x_{k}}}+\cdots }$$
где короткая форма ${\displaystyle u_{k,j}^{(0)}\equiv \partial u_{k}^{(0)}/\partial x_{j}}$ было использовано. Таким образом
$${\displaystyle {\frac {\partial P_{ij}}{\partial X_{j}}}\approx {\frac {\partial P_{ij}}{\partial x_{j}}}+u_{p.j}^{(0)}{\frac {\partial P_{ij}}{\partial x_{p}}}}$$
Предполагая далее, что статическая начальная деформация ${\displaystyle {\boldsymbol {u}}^{(0)}}$ (предварительно напряженное состояние) находится в равновесии, означает, что ${\displaystyle \operatorname {Div} {\boldsymbol {P}}^{(0)}={\boldsymbol {0}}}$, и закон движения может в сочетании с приведенным выше уравнением состояния быть сведен к линейному соотношению (т. е. где члены более высокого порядка в ${\displaystyle u_{m,n}^{(0)}}$) между статической начальной деформацией ${\displaystyle {\boldsymbol {u}}^{(0)}}$ и дополнительное динамическое возмущение ${\displaystyle {\boldsymbol {u}}^{(1)}({\boldsymbol {x}},t)}$ как (см. подробные выводы)
$${\displaystyle B_{ijkl}{\frac {\partial ^{2}u_{k}^{(1)}}{\partial x_{j}\partial x_{l}}}=\rho _{0}{\frac {\partial ^{2}u_{i}^{(1)}}{\partial t^{2}}},}$$
где
$${\displaystyle B_{ijkl}=C_{ijkl}+\delta _{ik}C_{jlqr}u_{q,r}^{(0)}+C_{rjkl}u_{i,r}^{(0)}+C_{irkl}u_{j,r}^{(0)}+C_{ijrl}u_{k,r}^{(0)}+C_{ijkr}u_{l,r}^{(0)}+C_{ijklmn}u_{m,n}^{(0)}.}$$
Это выражение распознается как линейное волновое уравнение. Рассматривая плоскую волну вида
$${\displaystyle {\boldsymbol {u}}^{(1)}({\boldsymbol {x}},t)={\boldsymbol {m}}\,f({\boldsymbol {N}}\cdot {\boldsymbol {x}}-ct),}$$
где ${\displaystyle {\boldsymbol {N}}}$ — единичный вектор Лагранжа в направлении распространения (т. е. параллельно волновому числу ${\displaystyle {\boldsymbol {k}}=k{\boldsymbol {N}}}$ нормаль к фронту волны), ${\displaystyle {\boldsymbol {m}}}$ — единичный вектор, называемый вектором поляризации (описывающий направление движения частицы), ${\displaystyle c}$ — скорость фазовой волны, а ${\displaystyle f}$ — дважды непрерывно дифференцируемая функция (например, синусоидальная функция). Вставка этой плоской волны в линейное волновое уравнение, полученное выше, дает
$${\displaystyle {\boldsymbol {Q}}({\boldsymbol {N}}){\boldsymbol {m}}=\rho _{0}c^{2}{\boldsymbol {m}}}$$
где ${\displaystyle {\boldsymbol {Q}}({\boldsymbol {N}})}$ вводится как акустический тензор и зависит от ${\displaystyle {\boldsymbol {N}}}$ как
$${\displaystyle [{\boldsymbol {Q}}({\boldsymbol {N}})]_{ik}=B_{ijkl}N_{j}N_{l}.}$$
Это выражение называется условием распространения и определяет для заданного направления распространения ${\displaystyle {\boldsymbol {n}}}$ скорость и поляризация возможных волн, соответствующих плоским волнам. Скорости волн можно определить по характеристическому уравнению
$${\displaystyle \det({\boldsymbol {Q}}({\boldsymbol {N}})-\rho _{0}c^{2}{\boldsymbol {I}})=0,}$$
где ${\displaystyle \det }$ — определитель, а ${\displaystyle {\boldsymbol {I}}}$ — единичная матрица.

Для гиперупругого материала ${\displaystyle {\boldsymbol {Q}}({\boldsymbol {N}})}$ равен симметричны (но не в общем случае), и собственные значения (${\displaystyle \rho _{0}c^{2}}$) таким образом, действительные. Чтобы скорости волн также были действительными, собственные значения должны быть положительными. Если это так, то для заданного направления распространения существуют три взаимно ортогональные действительные плоские волны ${\displaystyle {\boldsymbol {N}}}$. Из двух выражений акустического тензора ясно, что
$${\displaystyle \rho _{0}c^{2}={\boldsymbol {Q}}({\boldsymbol {N}}){\boldsymbol {m}}\cdot {\boldsymbol {m}}=B_{ijkl}N_{j}N_{l}m_{i}m_{k},}$$
и неравенство ${\displaystyle B_{ijkl}N_{j}N_{l}m_{i}m_{k}>0}$ (также называемое сильным условием эллиптичности) для всех ненулевых векторов ${\displaystyle {\boldsymbol {N}}}$ и ${\displaystyle {\boldsymbol {m}}}$ гарантируют, что скорость однородных плоских волн действительна. Поляризация ${\displaystyle {\boldsymbol {m}}={\boldsymbol {N}}}$ соответствует продольной волне, где движение частиц параллельно направлению распространения (также называется компрессионной волной). Две поляризации, где ${\displaystyle {\boldsymbol {m}}\cdot {\boldsymbol {N}}=0}$ соответствует поперечным волнам, в которых движение частиц ортогонально направлению распространения (также называемым сдвиговыми волнами).

Изотропные материалы

Модули упругости для изотропных материалов

Для изотропного тензора второго порядка (т. е. тензора, имеющего одинаковые компоненты в любой системе координат), такого как тензор деформации Лагранжа, ${\displaystyle {\boldsymbol {E}}}$ имеют инварианты ${\displaystyle \operatorname {tr} {\boldsymbol {E}}^{q}}$ где ${\displaystyle \operatorname {tr} }$ — оператор трассировки, а ${\displaystyle q\in \left\{1,2,3,\dots \right\}}$. Таким образом, функция энергии деформации изотропного материала может быть выражена как ${\displaystyle W({\boldsymbol {E}})=W(\operatorname {tr} {\boldsymbol {E}}^{q}),\,k\in \left\{1,2,3,\ldots \right\}}$ или их суперпозицию, которую можно переписать как
$${\displaystyle W={\frac {\lambda }{2}}(\operatorname {tr} {\boldsymbol {E}})^{2}+\mu \operatorname {tr} {\boldsymbol {E}}^{2}+{\frac {C}{3}}(\operatorname {tr} {\boldsymbol {E}})^{3}+B(\operatorname {tr} {\boldsymbol {E}})\operatorname {tr} {\boldsymbol {E}}^{2}+{\frac {A}{3}}\operatorname {tr} {\boldsymbol {E}}^{3}+\cdots ,}$$
где ${\displaystyle \lambda ,\mu ,A,B,C}$ являются константами. Константы ${\displaystyle \lambda }$ и ${\displaystyle \mu }$ — это модули упругости второго порядка, более известные как параметры Ламе, в то время как ${\displaystyle A,B,}$ и ${\displaystyle C}$ — это модули упругости третьего порядка, введенные , которые являются альтернативными, но эквивалентными ${\displaystyle l,m,}$ и ${\displaystyle n}$ введено Мурнаганом.
Объединяя это с общим выражением для функции энергии деформации, становится ясно, что
$${\displaystyle {\begin{aligned}C_{ijkl}&=\lambda \delta _{ij}\delta _{kl}+2\mu \delta I_{ijkl},\\C_{ijklmn}&=2C\delta _{ij}\delta _{kl}\delta _{mn}+2B(\delta _{ij}I_{klmn}+\delta _{kl}I_{mnij}+\delta _{mn}I_{ijkl})+{\frac {1}{2}}A(\delta _{ik}I_{jlmn}+\delta _{il}I_{jkmn}+\delta _{jk}I_{ilmn}+\delta _{jl}I_{ikmn}),\end{aligned}}\!\,}$$
где ${\displaystyle I_{ijkl}={\frac {1}{2}}(\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk})}$. Исторически использовался разный выбор этих упругих констант третьего порядка, и некоторые из вариаций показаны в Таблице 1.

Примеры значений для стали

В таблицах 2 и 3 представлены упругие константы второго и третьего порядка для некоторых типов сталей, представленных в литературе.

Акустоупругость при одноосном растяжении изотропных гиперупругих материалов

Кубовидный образец сжимаемого твердого тела в ненапряженной опорной конфигурации может быть выражен декартовыми координатами ${\displaystyle X_{i}\in [0,L_{i}],\,i=1,2,3}$, где геометрия выровнена с системой координат Лагранжа, и ${\displaystyle L_{i}}$ — длина сторон прямоугольного параллелепипеда в исходной конфигурации. Подвергая прямоугольный параллелепипед одноосному растяжению в ${\displaystyle x_{1}}$-направление так, чтобы оно деформировалось с чистой однородной деформацией, такой, что координаты материальных точек в деформированной конфигурации могут быть выражены как ${\displaystyle x_{1}=\lambda _{1}X_{1},x_{2}=\lambda _{2}X_{2},x_{3}=\lambda _{3}X_{3}}$, что дает
удлинения
$${\displaystyle e_{i}\equiv l_{i}/L_{i}-1=\lambda _{i}-1}$$
в ${\displaystyle x_{i}}$-направление. Здесь ${\displaystyle l_{i}}$ обозначает текущую (деформированную) длину стороны прямоугольного параллелепипеда ${\displaystyle i}$ и где отношение длины сторон в текущей и эталонной конфигурации обозначено как
$${\displaystyle \lambda _{i}\equiv l_{i}/L_{i}}$$
называемые основными участками. Для изотропного материала это соответствует деформации без какого-либо вращения (см. полярное разложение тензора градиента деформации, где ${\displaystyle {\boldsymbol {F}}={\boldsymbol {RU}}={\boldsymbol {VR}}}$ и поворот ${\displaystyle {\boldsymbol {R}}={\boldsymbol {I}}}$). Это можно описать через спектральное представление основными участками ${\displaystyle \lambda _{i}}$ как собственные значения или, что эквивалентно, удлинениями ${\displaystyle e_{i}}$.

Для одноосного растяжения в ${\displaystyle x_{1}}$-направлении (${\displaystyle P_{11}>0}$ мы предполагаем, что ${\displaystyle e_{1}}$ увеличиться на некоторую величину. Если боковые грани свободны от натяжения (т. е. ${\displaystyle P_{22}=P_{33}=0}$) боковые удлинения ${\displaystyle e_{2}}$ и ${\displaystyle e_{3}}$ ограничены диапазоном ${\displaystyle e_{2},e_{3}\in (-1,0]}$. Для изотропной симметрии боковые удлинения (или сокращения) также должны быть равны (т. е. ${\displaystyle e_{2}=e_{3}}$). Диапазон соответствует диапазону от полного бокового сокращения (${\displaystyle e_{2}=e_{3}=-1}$, что не является физическим), и к отсутствию изменений в боковых размерах (${\displaystyle e_{2}=e_{3}=0}$). Отмечено, что теоретически диапазон может быть расширен до значений, больших 0, соответствующих увеличению поперечных размеров в результате увеличения осевого размера. Однако очень немногие материалы (называемые ауксетическими материалами) демонстрируют это свойство.

Расширение скоростей звука

Если условие сильной эллиптичности (${\displaystyle B_{ijkl}N_{j}N_{l}m_{i}m_{k}>0}$) имеет место, три ортогональных направления поляризации (${\displaystyle {\boldsymbol {m}}}$ даст ненулевую и действительную скорость звука для заданного направления распространения ${\displaystyle {\boldsymbol {N}}}$. Ниже будут получены скорости звука для одного выбора приложенного одноосного натяжения, направления распространения и ортонормального набора векторов поляризации. Для одноосного натяжения, приложенного в ${\displaystyle x_{1}}$-направлении и вывод скоростей звука для волн, распространяющихся перпендикулярно приложенному натяжению (например, в ${\displaystyle x_{3}}$-направлении с вектором распространения ${\displaystyle {\boldsymbol {N}}=[0,0,1]}$), один выбор ортонормальных поляризаций может быть
$${\displaystyle \{{\boldsymbol {m}}\}={\begin{cases}\mathbf {m} _{1}=\mathbf {\hat {x}} _{1}=[1,0,0]&\|\,{\text{to applied tension}}\\\mathbf {m} _{2}=\mathbf {\hat {x}} _{2}=[0,1,0]&\perp {\text{to applied tension}}\\\mathbf {m} _{3}=\mathbf {\hat {x}} _{3}=[0,0,1]&\|\,{\textrm {to}}\,\mathbf {N} \end{cases}}}$$
что дает три скорости звука
$${\displaystyle \rho _{0}c_{33}^{2}=B_{3333},\qquad \rho _{0}c_{31}^{2}=B_{1313},\qquad \rho _{0}c_{32}^{2}=B_{2323},}$$
где первый индекс ${\displaystyle i}$ скоростей звука ${\displaystyle c_{ij}}$ указывает направление распространения (здесь ${\displaystyle x_{3}}$-direction, в то время как второй индекс ${\displaystyle j}$ указывает выбранное направление поляризации (${\displaystyle j=i}$ соответствует движению частицы в направлении распространения ${\displaystyle i}$ – т.е. продольная волна, а ${\displaystyle j\neq i}$ соответствует движению частицы перпендикулярно направление распространения – т. е. сдвиговая волна).

Разложение соответствующих коэффициентов акустического тензора и замена модулей упругости второго и третьего порядка ${\displaystyle C_{ijkl}}$ и ${\displaystyle C_{ijklmn}}$ с их изотропными эквивалентами, ${\displaystyle \lambda ,\mu }$ и ${\displaystyle A,B,C}$ соответственно, приводит к скоростям звука, выраженным как
$${\displaystyle \rho _{0}c_{33}^{2}=\lambda +2\mu +a_{33}e_{1},\qquad \rho _{0}c_{3k}^{2}=\mu +a_{3k}e_{1},\quad k=1,2}$$
где
$${\displaystyle a_{33}=-{\frac {2\lambda (\lambda +2\mu )+\lambda A+2(\lambda -\mu )B-2\mu C}{\lambda +\mu }}}$$
$${\displaystyle a_{31}={\frac {(\lambda +2\mu )(4\mu +A)+4\mu B}{4(\lambda +\mu )}}}$$
$${\displaystyle a_{32}=-{\frac {\lambda (4\mu +A)-2\mu B}{2(\lambda +\mu )}}}$$
– коэффициенты акустоупругости, связанные с эффектами упругих постоянных третьего порядка.

Методы измерения

Чтобы иметь возможность измерить скорость звука, а точнее изменение скорости звука, в материале, подверженном некоторому напряженному состоянию, можно измерить скорость акустического сигнала, распространяющегося через рассматриваемый материал. Существует несколько методов сделать это, но все они используют одно из двух физических соотношений скорости звука. Первое соотношение связано со временем, которое требуется сигналу для распространения из одной точки в другую (обычно это расстояние между двумя акустическими преобразователями или двукратное расстояние от одного преобразователя до отражающей поверхности). Это часто называют измерениями «времени пролета» (TOF) и используют отношение $${\displaystyle c={\frac {d}{t}}}$$ где ${\displaystyle d}$ — это расстояние, которое проходит сигнал, а ${\displaystyle t}$ — это время, необходимое для прохождения этого расстояния. Второе соотношение связано с обратной величиной времени, частотой сигнала. Соотношение здесь следующее: $${\displaystyle c=f\lambda }$$ где ${\displaystyle f}$ — частота сигнала, а ${\displaystyle \lambda }$ — длина волны. Измерения с использованием частоты в качестве измеряемой величины используют явление акустического резонанса, где ${\displaystyle n}$ количество длин волн соответствует длине, на которой резонирует сигнал. Оба эти метода зависят от расстояния, на котором он измеряется, либо напрямую, как в методе времени пролета, либо косвенно, через соответствие количества длин волн на физическом протяжении образца, которые резонируют.

Пример методов ультразвукового контроля

В общем, существует два способа настройки системы преобразователей для измерения скорости звука в твердом теле. Один из них — это установка с двумя или более преобразователями, где один действует как передатчик, а другой(ие) действует как приемник. Измерение скорости звука может быть выполнено путем измерения времени между генерацией сигнала на передатчике и его регистрацией на приемнике, при этом предполагается, что известно (или измерено) расстояние, которое акустический сигнал прошел между преобразователями, или, наоборот, для измерения резонансной частоты, зная толщину, на которой резонирует волна. Другой тип установки часто называют системой импульс-эхо. Здесь один преобразователь размещается вблизи образца, действуя как передатчик и приемник. Для этого требуется отражающий интерфейс, где сгенерированный сигнал может отражаться обратно к преобразователю, который затем действует как приемник, регистрирующий отраженный сигнал. См. ультразвуковое тестирование для некоторых систем измерения.

Продольные и поляризованные сдвиговые волны

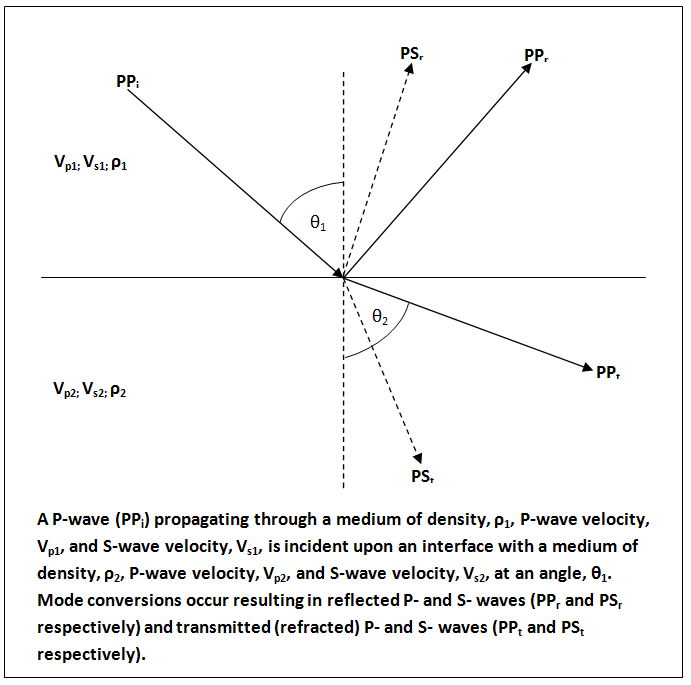
Как объяснялось выше, набор из трех ортонормальных поляризаций (${\displaystyle {\boldsymbol {m}}}$) движения частицы существует для заданного направление распространения ${\displaystyle {\boldsymbol {N}}}$ в твердом теле. Для измерительных установок, где преобразователи могут быть зафиксированы непосредственно на исследуемом образце, возможно создать эти три поляризации (одну продольную и две ортогональные поперечные волны) путем применения различных типов преобразователей, возбуждающих требуемую поляризацию (например, пьезоэлектрические преобразователи с необходимым режимом колебаний). Таким образом, можно измерить скорость звука волн со всеми тремя поляризациями с помощью зависящих от времени или частоты измерительных установок в зависимости от выбора типов преобразователей. Однако, если преобразователь не может быть зафиксирован на испытуемом образце, необходима связующая среда для передачи акустической энергии от преобразователя к образцу. В качестве этой связующей среды часто используются вода или гели. Для измерения продольной скорости звука этого достаточно, однако жидкости не переносят сдвиговых волн, и, таким образом, чтобы иметь возможность генерировать и измерять скорость сдвиговых волн в испытуемом образце, падающая продольная волна должна взаимодействовать под косым углом с поверхностью жидкости/твердого тела для генерации сдвиговых волн посредством преобразования мод. Затем такие сдвиговые волны преобразуются обратно в продольные волны на поверхности твердого тела/жидкости, распространяющиеся обратно через жидкость к регистрирующему преобразователю, что позволяет также измерять скорости сдвиговых волн через связующую среду.

Приложения

Инженерные материалы – оценка напряжений

Поскольку отрасль стремится сократить расходы на техническое обслуживание и ремонт, неразрушающий контроль конструкций становится все более ценным как в производственном контроле, так и в качестве средства измерения использования и состояния ключевой инфраструктуры. Существует несколько методов измерения для измерения напряжения в материале. Однако методы, использующие оптические измерения, магнитные измерения, рентгеновскую дифракцию и нейтронную дифракцию, ограничены измерением поверхностного или околоповерхностного напряжения или деформации. Акустические волны легко распространяются через материалы и, таким образом, предоставляют средство для исследования внутренней части конструкций, где уровень напряжения и деформации важен для общей структурной целостности. Поскольку скорость звука таких нелинейных упругих материалов (включая обычные строительные материалы, такие как алюминий и сталь) зависит от напряжения, одним из применений акустоупругого эффекта может быть измерение напряженного состояния внутри нагруженного материала с использованием различных акустических зондов (например, ультразвукового контроля) для измерения изменения скорости звука.

Сыпучие и пористые материалы – геофизика

Сейсмология изучает распространение упругих волн через Землю и используется, например, в исследованиях землетрясений и при картировании недр Земли. Недра Земли подвергаются различным давлениям, и поэтому акустические сигналы могут проходить через среды в различных напряженных состояниях. Таким образом, акустоупругая теория может представлять практический интерес, когда нелинейное поведение волн может использоваться для оценки геофизических свойств.

Мягкие ткани – медицинский ультразвук

Другие приложения могут быть в медицинской сонографии и эластографии, измеряя уровень напряжения или давления в соответствующих типах эластичных тканей
(например,

), улучшая неинвазивную диагностику.