Коэффициент Пуассона: что это и как он влияет на материалы
Коэффициент Пуассона — это важная характеристика материалов, которая помогает понять, как они деформируются под нагрузкой. Этот параметр играет ключевую роль в материаловедении, механике и инженерии, особенно при проектировании конструкций, машин и других объектов, которые должны выдерживать механические нагрузки. В этой статье мы разберем, что такое коэффициент Пуассона, как он работает, и почему он так важен для промышленности и науки.
Что такое коэффициент Пуассона?
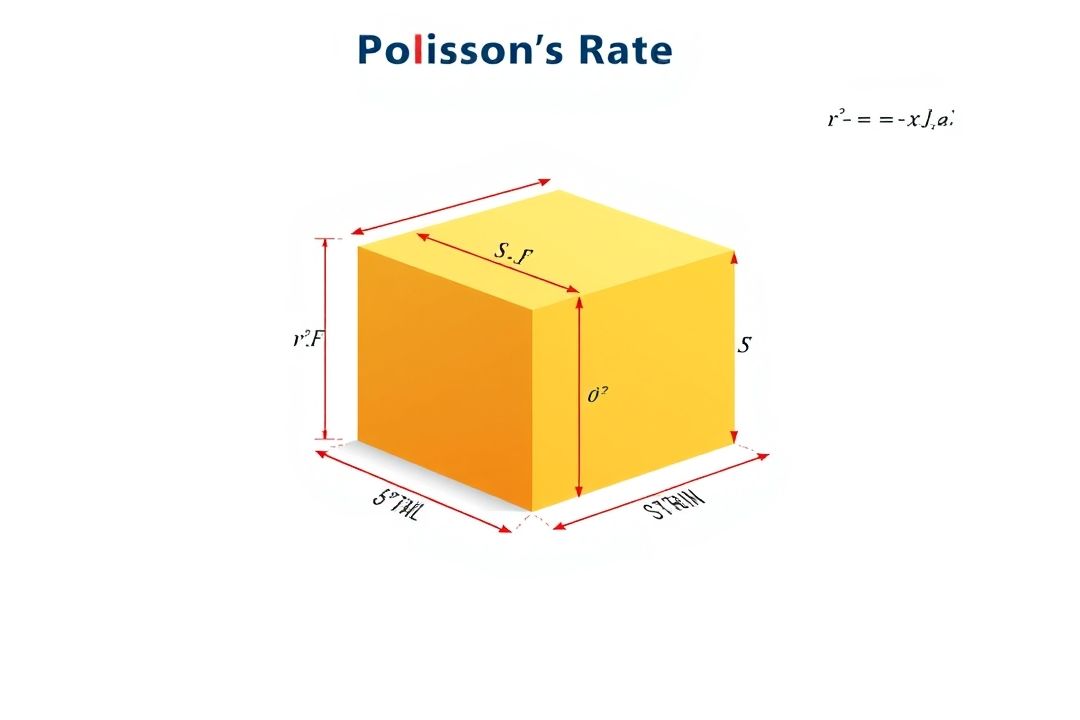
Коэффициент Пуассона (обозначается греческой буквой ν) — это мера, которая показывает, как материал деформируется в поперечном направлении при растяжении или сжатии вдоль одной оси. Проще говоря, если вы растягиваете резиновую ленту, она становится тоньше. Это и есть эффект Пуассона.
Коэффициент Пуассона определяется как отношение поперечной деформации к продольной. Если материал сжимается вдоль одной оси, он расширяется в поперечных направлениях, и наоборот. Например, если вы сжимаете кубик материала, его стороны будут выпирать.
Как рассчитывается коэффициент Пуассона?
Формула для расчета коэффициента Пуассона выглядит так:
ν = — (ε_поперечная / ε_продольная)
Где:
— ε_поперечная — деформация в поперечном направлении,
— ε_продольная — деформация в продольном направлении.
Отрицательный знак в формуле указывает на то, что поперечная деформация происходит в противоположном направлении относительно продольной.
Диапазон значений коэффициента Пуассона
Коэффициент Пуассона может принимать значения от -1 до 0,5. Большинство материалов имеют положительный коэффициент Пуассона, что означает, что при растяжении они сужаются в поперечном направлении, а при сжатии — расширяются.
— Резина: Коэффициент Пуассона близок к 0,5, что указывает на почти несжимаемость материала.
— Металлы: Обычно имеют значения от 0,2 до 0,35. Например, для стали это около 0,3.
— Пенопласты и пористые материалы: Могут иметь коэффициент Пуассона близкий к 0, так как их структура позволяет сжиматься без значительного расширения в поперечном направлении.
— Ауксетики: Это материалы с отрицательным коэффициентом Пуассона. При растяжении они расширяются в поперечном направлении, что делает их уникальными и полезными для специальных применений.
Эффект Пуассона в природе и технике
Эффект Пуассона проявляется в различных областях. Например, при проектировании трубопроводов важно учитывать, как трубы будут расширяться или сжиматься под давлением. Если жидкость или газ внутри трубы находятся под высоким давлением, это вызывает кольцевое напряжение в стенках трубы, что приводит к увеличению диаметра и небольшому уменьшению длины.
В геологии эффект Пуассона объясняет, как горные породы деформируются под действием тектонических сил.
