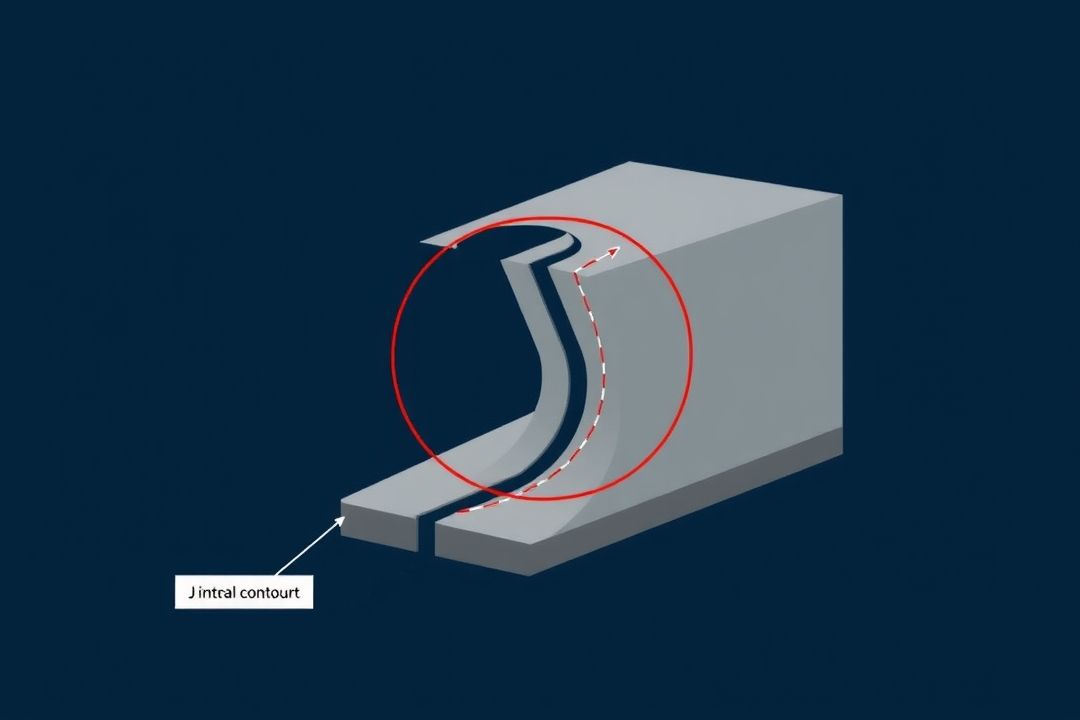
Что такое J-интеграл и зачем он нужен?
J-интеграл — это важный инструмент в механике разрушения, который позволяет оценить скорость выделения энергии деформации на единицу площади поверхности разрушения в материале. Эта концепция была разработана независимо двумя учеными: Г. П. Черепановым в 1967 году и Джеймсом Р. Райсом в 1968 году. Райс доказал, что энергетический контурный интеграл, обозначаемый как J, не зависит от пути вокруг трещины. Это открытие стало ключевым для анализа разрушения материалов, особенно в случаях, когда традиционные методы линейной механики упругого разрушения (LEFM) оказываются недостаточно точными.
J-интеграл используется для оценки критических свойств разрушения материалов, особенно когда размеры образцов слишком малы для применения LEFM. Экспериментальные методы, основанные на J-интеграле, позволяют определить вязкость разрушения материала через критическое значение энергии разрушения JIc. Это значение указывает на момент, когда в материале начинается крупномасштабное пластическое течение при распространении трещины в режиме I (растяжение).
J-интеграл равен скорости выделения энергии деформации для трещины в теле, подвергнутом монотонному нагружению. В квазистатических условиях это справедливо для линейно-упругих материалов. Однако для материалов, которые испытывают небольшую текучесть на вершине трещины, J-интеграл также может быть использован для расчета скорости выделения энергии в определенных условиях, таких как монотонная нагрузка в режиме III (антиплоский сдвиг).
Основные принципы J-интеграла
Одним из ключевых свойств J-интеграла является его независимость от пути для линейно-упругих материалов. Это означает, что значение J-интеграла не зависит от выбора контура вокруг трещины. Однако для упругопластических материалов это свойство сохраняется только при определенных условиях, таких как монотонная нагрузка без пластической разгрузки. Если нагрузка становится непропорциональной, J-интеграл начинает зависеть от пути.
Двумерный J-интеграл определяется через плотность энергии деформации W(x₁, x₂), вектор поверхностного сцепления t = [σ]n, где σ — тензор напряжений Коши, n — нормаль к кривой Γ, и вектор смещения u. Плотность энергии деформации рассчитывается как функция напряжений и деформаций в материале.
Применение J-интеграла в механике разрушения
J-интеграл широко используется для анализа напряжений и деформаций вблизи вершина трещины в нелинейно-упругих и упругопластических материалах. Райс показал, что при монотонной нагрузка J-интеграл можно использовать для расчета скорости выделения энергии даже в пластических материалах. Это особенно полезно для материалов, которые испытывают небольшую текучесть на вершине трещины.
Для изотропных, хрупких, линейно-упругих материалов J-интеграл напрямую связан с вязкостью разрушения. Например, для плоской деформации в режиме I нагружения это соотношение выражается через критическую скорость выделения энергии GIc и коэффициент интенсивности напряжений KIc. Аналогичные соотношения существуют для режимов II и III нагружения.
J-интеграл и пластические материалы
В случае упругопластических материалов J-интеграл характеризует сингулярные поля напряжений и деформаций на вершине трещины. Хатчинсон, Райс и Розенгрен показали, что J-интеграл можно использовать для описания полей напряжений и деформаций в материалах с степенным упрочнением, где размер пластической зоны мал по сравнению с длиной трещины.
Модель Хатчинсона основана на материальном конститутивном законе, предложенном Рамбергом и Осгудом. Эта модель описывает зависимость напряжения от деформации для материалов, которые подвергаются монотонному нагружению без разгрузки. Она параметризуется коэффициентом наклепа n и безразмерной постоянной α, которая характеризует материал.
Практическое применение J-интеграла
J-интеграл находит широкое применение в промышленности и производстве, особенно в областях, связанных с анализом прочности и долговечности материалов. Например, он используется для оценки критических нагрузок, при которых начинается разрушение конструкций, таких как мосты, самолеты или трубопроводы. Это позволяет инженерам проектировать более безопасные и надежные конструкции.
Кроме того, J-интеграл используется в материаловедении для изучения свойств новых материалов, таких как композиты или сплавы с повышенной прочностью. Это помогает определить, как материалы будут вести себя под нагрузкой и при каких условиях они начнут разрушаться.
Преимущества J-интеграла перед другими методами
Одним из главных преимуществ J-интеграла является его универсальность. В отличие от линейной механики упругого разрушения, которая применима только для хрупких материалов, J-интеграл может быть использован для анализа как упругих, так и пластических материалов. Это делает его незаменимым инструментом для изучения сложных материалов, которые сочетают в себе свойства упругости и пластичности.
Кроме того, J-интеграл позволяет учитывать нелинейные эффекты, такие как пластическая деформация, что делает его более точным методом для анализа реальных материалов, которые редко бывают идеально упругими.
Ограничения J-интеграла
Несмотря на свои преимущества, J-интеграл имеет и некоторые ограничения. Например, он применим только для монотонных нагрузок без разгрузки. Если материал подвергается циклическим нагрузкам или разгрузке, J-интеграл может дать некорректные результаты. Кроме того, для сложных геометрий или многокомпонентных материалов расчет J-интеграла может быть затруднен.
